A photovoltaic device’s spectral response $$SR$$ is what relates the device’s short circuit current $$I_{sc}$$ to the incident spectral irradiance $$E(\lambda)$$:
$$I_{sc} \propto \int_{0}^{\infty} E(\lambda) SR(\lambda) \mathrm{d} \lambda$$
However, using spectral irradiance to estimate device output in absolute terms like this is not common in practice. What is more typical is to have separate modeling steps for the effect of overall irradiance level (e.g., the reading from a thermopile pyranometer) and that of spectral distribution (for example whether the light is redder or bluer). The latter is quantified as a unitless coefficient called the spectral modifier, spectral adjustment, or spectral factor, and represents the performance difference under some spectrum of interest relative to the reference spectrum of AM1.5G.
The spectral modifier $$MM$$ is calculated as the ratio of integrals of the above form, with secondary normalization integrals to remove the effect of absolute irradiance level:
$$
MM = \frac{
\int_{0}^{\infty} E(\lambda) SR(\lambda) \mathrm{d} \lambda
}{
\int_0^{\infty} E(\lambda) \mathrm{d}\lambda
}
\frac{
\int_0^{\infty} E_{ref}(\lambda) \mathrm{d}\lambda
}{
\int_{0}^{\infty} E_{ref}(\lambda) SR(\lambda) \mathrm{d} \lambda
}
$$
Example daily spectral modifier values for a dataset of global normal spectral irradiance measurements, assuming typical spectral response curves for crystalline silicon (Si) and thin film cadmium telluride (CdTe) cells, are shown below:
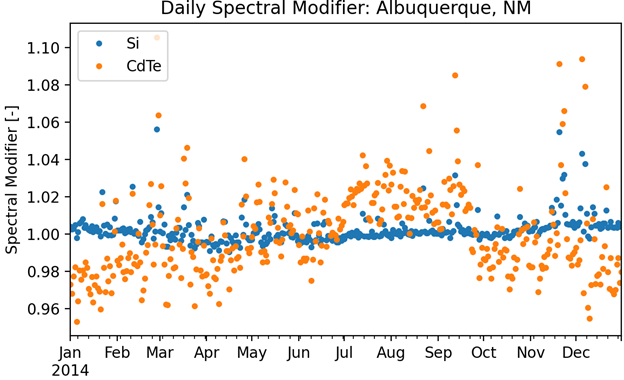
Spectral modifier values can be calculated from incident spectra and spectral response curves using the pvlib-python function pvlib.spectrum.calc_spectral_mismatch_field.
References
[1] Anton Driesse and Joshua S. Stein, “Global normal spectral irradiance in Albuquerque: a one-year open dataset for PV research”. 2020. SAND2020-12693.