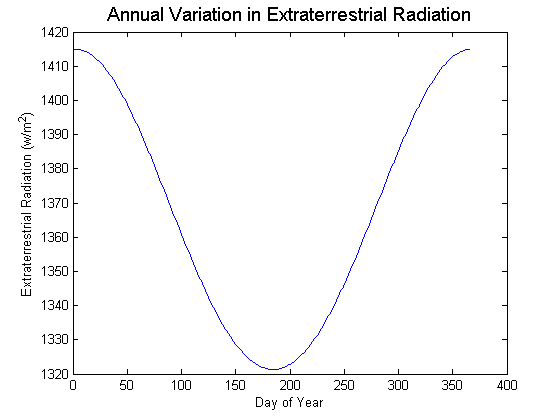
Extraterrestrial radiation () is the intensity (power) of the sun at the top of the Earth’s atmosphere. It is usually expressed in irradiance units (Watts per square meter) on a plane normal to the sun. It varies throughout the year because of the Earth’s elliptical orbit, which results in the Earth-Sun distance varying during the year in a predictable way. This effect can be represented empirically with the following equations:
, where
is the solar constant (
).
is the mean sun-earth distance and
is the actual sun-earth distance depending on the day of the year.
, where
,
where is the day of the year (integer).
