The Sandia PV Array Performance Model (SAPM) defines five points on the IV curve. These points are shown in the figure below.
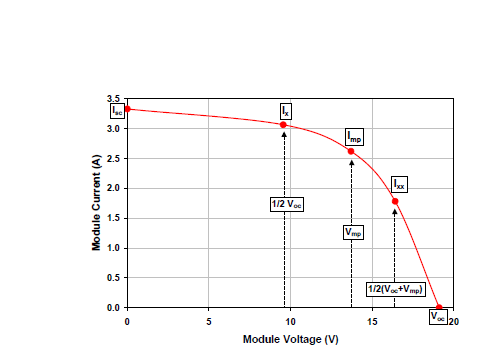
The SAPM defines the primary points ($$I_{sc}$$, $$I_{mp}$$, $$V_{oc}$$, and $$V_{mp}$$) with the following equations:
$$I_{sc}=I_{sc0}\times f_{1} \left ( \frac{E_{b}f_{2}+f_{d}E_{d}}{E_{0}} \right )\times \left ( 1+\alpha _{Isc}\left ( T_{c}-T_{0} \right ) \right )$$ (eq. 1)
$$I_{mp}=I_{mp0}\left ( C_{0}E_{e}+C_{1}{E_{e}}^{2} \right )\left ( 1+\alpha _{Imp}\left ( T_{c}-T_{0} \right )\right )$$ (eq. 2)
$$V_{oc}=V_{oc0}+N_{s}\delta \ln \left ( E_{e} \right )+\beta _{Voc}\left ( T_{c}-T_{0} \right )$$ (eq. 3)
$$V_{mp}=V_{mp0}+C_{2}N_{s}\delta \ln \left ( E_{e} \right )+C_{3}N_{s}\left ( \delta \ln \left ( E_{e} \right ) \right )^{2}+\beta _{Vmp}\left ( T_{c} -T_{0}\right )$$ (eq. 4)
Functions:
$$f_1$$ is a 4th order polynomial function of absolute air mass, $$AM_a$$, and is called the air mass modifier. It is defined as:
$$f_{1}\left ( AM_{a} \right )=a_{0}+a_{1}AM_{a}+a_{2}\left ( AM_{a} \right )^{2}+a_{3}\left ( AM_{a} \right )^{3}+a_{4}\left ( AM_{a} \right )^{4}$$
where $$a$$ is the vector of coefficients that are determined from module testing.
$$f_2$$ is a 5th order polynomial function of angle of incidence, $$AOI$$, and is called the angle of incidence modifier. it is defined as:
$$f_{2}\left ( AOI \right )=b_{0}+b_{1}AOI+b_{2}\left ( AOI \right )^{2}+b_{3}\left ( AOI \right )^{3}+b_{4}\left ( AOI \right )^{4}+b_{5}\left ( AOI \right )^{5}$$
where $$b$$ is the vector of coefficients that are determined from module testing.
$$E_e$$ is the “effective irradiance”. It is defined as:
$$E_{e}=\frac{I_{sc}}{I_{sc0}\left \{ 1+\alpha _{Isc}\left ( T_{c}-T_{0} \right ) \right \}}$$, where:
- $$I_{sc0}$$ is the short circuit current at reference conditions.
- $$I_{sc}$$ can be calculated from (eq. 1) above.
$$\delta$$ is a function of $$T_{c}$$ defined as: $$\delta =\frac{n\times k\left ( T_{c}+273.15 \right )}{q}$$, where:
- $$n$$ is an empirically determined ‘diode factor’,
- $$k$$ is Boltzmann’s constant ($$1.38066\times 10^{-23}J/K$$),
- $$q$$ is the elementary charge constant ($$1.60218\times 10^{-19}coulomb$$)
$$\beta_{Voc}$$ is a function of effective irradiance,$$E_e$$ , defined as: $$\beta _{Voc}=\beta _{Voc0}+m_{\beta Voc}\left ( 1-E_{e} \right )$$, where:
- $$\beta_{Voc0}$$ is the temperature coefficient for module open circuit voltage at irradiance conditions of $$1000 W/m^2$$ .
- $$m_{\beta Voc}$$ is a coefficient describing the irradiance dependence for the open circuit voltage temperature coefficient (typically equals zero)
Parameters:
- $$E_{b}$$ is beam irradiance on the plane of array
- $$E_{d}$$ is the diffuse irradiance on the plane of array
- $$E_{0}$$ is reference solar irradiance ($$1000 W/m^2$$)
- $$T_{c}$$ is cell temperature ($$^{\circ}C$$)
- $$T_{0}$$ is reference cell temperature ($$25^{\circ}C$$)
- $$f_{d}$$ is the fraction of the diffuse light that is used by the module. For typical flat plate modules $$f_{d}$$ is usually assumed to be equal to 1. For concentrators the value can be smaller than 1.
- $$\alpha_{lsc}$$ is the normalized temperature coefficient for short circuit current. Units are $$1/^{\circ}C$$
- $$\alpha_{lmp}$$ is the normalized temperature coefficient for maximum power current. Units are $$1/^{\circ}C$$
- $$N_{s}$$ is the number of cells in series
- $$C$$ is a vector of coefficients determined by module testing using a method developed at Sandia.
Reference
- King, D. L., E. E. Boyson and J. A. Kratochvil (2004). Photovoltaic Array Performance Model. Albuquerque, NM, Sandia National Laboratories. SAND2004-3535. Link