Air mass is a relative measure of the optical length of the atmosphere. At sea level, when the sun is directly overhead (zenith angle = 0), the air mass is equal to 1. As the zenith angle becomes larger, the path of direct sunlight through the atmosphere grows longer and air mass increases. “Relative” air mass is only a function of sun position and assumes the observer is at sea level.
The simplest estimate of relative air mass (ignoring land elevation effects) assumes a spherical earth and atmosphere. The relative air mass is simply a trigonometric function of the zenith angle:
$$AM=\frac{1}{cos(\Theta_z)}$$ or $$AM={sec}(\Theta_z)$$, where $$\Theta_z$$ is the solar zenith angle.
This simple approximation is quite accurate for zenith angles less than 80 degrees. When the sun is near the horizon, more complex and accurate models are warranted.
The PV_LIB Toolbox has a function pvl_relativeairmass that implements several of the more accurate models available. The figure below shows a comparison between seven model forms available in the literature.
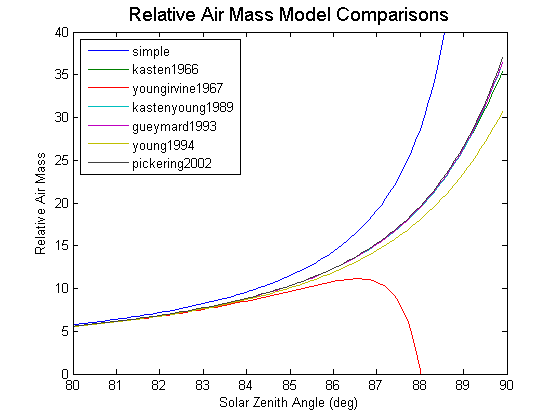
“Absolute” air mass is relative air mass that is corrected to account for atmospheric pressure, which thus accounts for elevation and weather effects. The PV_LIB Toolbox has a function pvl_absoluteairmass that implements this empirical correction.