Spectral Mismatch Models

You are here:

Spectral mismatch models are part of the translation from broadband plane-of-array (POA) irradiance to effective irradiance. Generally, the translation takes the form

$E_e = M \times \{ IAM_B \times E_b + E_{diff} \} \times SF$

where $M$ is the spectral mismatch modifier, $IAM_B$ is the reflection losses for the beam irradiance $E_b$ (i.e., $DNI \times \cos(AOI)$ ) , $E_{diff}$ is the diffuse POA irradiance and $SF$ is the soiling factor. Models for $IAM_B$ are found here.

Air mass model for M

A polynomial may be fit to concurrent measurements of effective irradiance $E_e$ and absolute air mass $AM_a$ to model $M$ . The polynomial model has the advantage of simplicity: air mass $AM_a$ can be modeled from ephemeris. However, care should be taken when applying this model outside the range of data used to fit the model.

In the SAPM, a 4th degree polynomial $f_1(AM_a)$ is fit to data and the coefficients are normalized so that $f_1(AM_a = 1.5) = 1$ :

$f_1 (AM_a) = \alpha_0 + \alpha_1 \times AM_a + \alpha_2 \times AM_a^2 + \alpha_3 \times AM_a^3 + \alpha_4 \times AM_a^4$

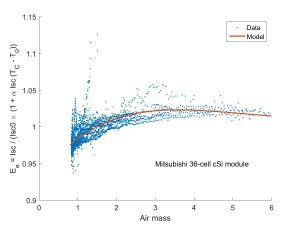
This approach is adopted in the De soto et al. performance model , and is illustrated here for a c-Si module.

Model for M using air mass and precipitable water

An alternative model is presented by M. Lee and A. Panchula (2016), where $M$ is modeled using air mass and estimated precipitable water:

$M = b_0 + b_1 \times AM_a + b_2 \times p_{wat} + b_3 \times \sqrt{AM_a} + b_4 \times \sqrt{p_{wat}} + b_5 \times \frac{AM_a}{\sqrt{p_{wat}}}$

where $p_{wat}$ is precipitable water (cm) which can be estimated from ambient temperature and relative humidity using an appropriate model (e.g., pvl_calcPwat). Coefficients for this model are found in PVLib function pvl_FSspeccorr.m.