A series of papers by Martin and Ruiz (2001; 2002; 2004) describe the optical reflectance loss for PV modules and model the effect of these losses on annual energy.
Martin and Ruiz (2001) establish that the angular losses (AL) of a PV modules are a function of the solar incident angle ($$\theta_{AOI}$$).
$$AL(\theta_{AOI}) = 1-\frac {\overline{T}(\theta_{AOI} )}{\overline{T}(0)}=1-\left [ \frac{1-\exp(-\cos(\theta_{AOI})/a_r)}{1-\exp(-1/a_r)} \right]\cong 1-\frac{1-\overline{R}(\theta_{AOI})}{1-\overline{R}(0)}$$
where T(x) is the weighted transmittance at incident angle x, R(x) is the weighted reflectance at incident angle x, and $$a_r$$ is the angular losses coefficient, an empirical dimensionless parameter to fit in each case.
An angular factor, $$f_{I\alpha}$$ , is defined by the ratio of the PV module’s short circuit current, $$O_{sc}$$, at incident angle $$\theta_{AOI}$$ to the $$I_{sc}$$ at normal incidence:
$$f_{I\alpha} = \frac {I_{sc} (\theta_{AOI})}{I_{sc}(0) \cos(\theta_{AOI})}\cong \frac{1-\overline{R}(\theta_{AOI})}{1-\overline{R}(0)}$$
This angular factor is the incident angle modifier.
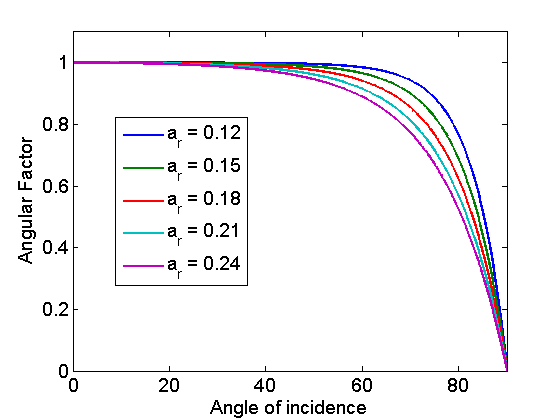
The angular factor can be experimentally determined for a finite number of incidence angles, $$\theta_{AOI}$$, and the data may be used to fit an appropriate angular losses coefficient, $$a_r$$, to determine the angular factor for any incident angle.
It should be noted that when experimentally determining $$f_{I\alpha}$$, the light source must be collimated (beam irradiance).
Sample results of the Martin & Ruiz model for varying $$a_r$$
References
[1] Martin, N., Ruiz, J. M. Calculation of the PV modules angular losses under field conditions by means of an analytical model. Solar Energy Materials & Solar Cells 70, pp. 25-38.
[2] Martin, N., Ruiz, J. M. A New Model for PV Modules Angular Losses Under Field Conditions. International Journal of Solar Energy, 2002, Vol. 22(1), pp. 19-31
[3] Martin, N., Ruiz, J. M. Annual Angular Reflection Losses in PV Modules. Progress in Photovoltaics: Research and Applications. 2005; 13:75-84.
